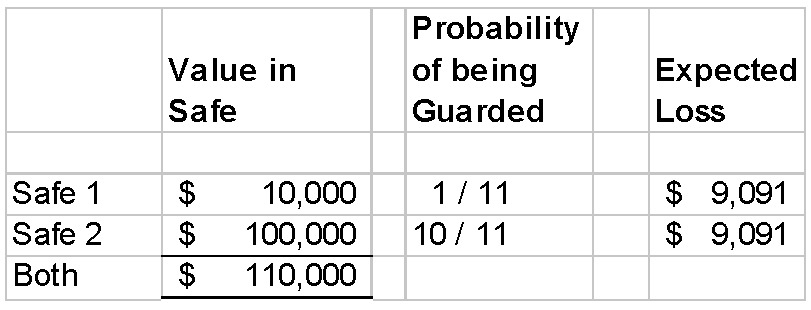
Figure #8.2: Mixed Strategy Calculation

Expected value is calculated as follows:

Expected value = probability of success x value of success.

The expected value of the thief getting (the guard losing) the $10,000 from safe 1 when the guard is protecting safe 1 1/11 of the time is

$9,091 = (1 - 1/11) x $10,000 .

The expected value of the thief getting (the guard losing) the $100,000 from safe 2 when the guard is protecting safe 2 10/11 of the time is

$9,091 = (1 - 10/11) x $100,000 .

This says that in the guards mixed strategy situation the thief can expect to get $9,091 regardless of which safe he chooses to rob. The thief himself will probably want to employ a mixed strategy since he doesn't want to become predictable (assuming an iterated game) and get foiled by a guard who figures his strategy choice out.

This compares to the pure strategy solution, which is...

The expected value of the thief getting (the guard losing) the $10,000 from safe 1 when the guard is protecting only safe 2 is

$10,000 = 100% x $10,000 .