|
List of Figures, Diagrams & Pictures |
Figure #2: Key Area of Interest
Figure #3: Dominating Strategy
Figure #4: Eliminate any Dominated Strategy - Simple example
Figure #5: Eliminate any Dominated Strategy - Complex example
Figure #6: Looking for the Minimax/ Maximin values
Figure #7: Nash equilibrium and the Boxed Pigs Game
Figure #7-2: Boxed Pigs Example
Figure #8-2: Mixed Strategy Calculation
Figure #10: Payoff Matrix for Hawk/Dove Game
Figure #11: ESS of Hawk/Dove Game
|
Introduction |
In these webnotes we will provide you with brief, intuitive description of game theory. Although, game theory is actually a highly mathematical field requiring knowledge of such disciplines as set theory, probability theory and linear algebra; the basic concepts are not difficult to describe using only simple mathematics.
We will be generally limiting our discussions to games with only 2 players; however, games with more players are possible. Having more players in the game creates not only an additional algebraic complexity but also an additional logical complexity. For example, in a three player game two of the players could form an alliance against the third player.
We will start our webnotes by explaining some key game theory terms and answering some basic questions about game theory. This should give you sufficient background knowledge to understand the topics that we discuss in the rest of the notes. Then, we discuss types of games. Here, it is important that you understand that different types of games can produce different types of results and can employ different types of strategies. Next, we analyze some of the basic game solving techniques. Hopefully, the pictures we have used here allow you to gain a quick understanding of these items. Evolutionary concepts come next. In this section we explain games where we look for players who employ strategies which can be stable over time. In particular, we analyze the hawk/dove game. Then, we take a quick look at where game theory is used and what limitations and problems game theory has. Finally, we provide a summary of the major concepts that we have covered in the notes. This summary is in the form of an alphabetic glossary. (If you are in a hurry to understand game theory, you might want to start at the summary.)
|
Background |
We assume humans are rational beings and we always seek the best alternative in a set of possible choices. This assumption is needed to have even the possibility of constructing mathematical theories to analyze game strategies.
The rationality assumption also serves two major purposes:
Predictability. To formulate theories, we have to be able to generate valid rules. Predictability helps us to presume the motive of the opponent.
Utility theory is based on rationality, since all moves made in a game is assumed to be rational choices. Secondly, utility theory assumes maximization of utility. Both players of a game are assumed to attempt maximization of their profit. "Maximization" is relative to a player's goal.
For example, few people would risk a sure gain of $1,000,000 for an even chance of gaining $10,000,000.
This indicates that they are not maximizing their average profit. Hence game theory does not attempt to indicate what a player's goal is, but rather attempts to "maximize" whatever player intended goal is. Von Neumann and Morgenstern understood this distinction in 1944.
Utility theory is a quantification of a person's preferences with respect to certain objects. For example, different people will assign different preferences to coffee and tea.
Game theory is a study of how to mathematically determine the best strategy for given conditions in order to optimize the outcome.
It focuses on how groups of people interact, in which people have to predict how their opponents will react to their moves. Game theory achieves through mathematical formulas.
It finds acceptable, if not optimal, strategies in conflict situations. Since optimal solutions may not always be possible, predictions about the opponent's move have to be made. Also, it is an abstraction of real complex situation. Computers can only deal with concrete mathematical terms. Coding input in mathematical terms (called payoff values) is required.
Game theory utilizes mathematical principles, in order to emulate human value judgement and intangible rules.
Game theory assumes all human interactions can be understood and navigated by presumptions.
All intelligent beings make decisions all the time. To emulate human behavior, AI needs to perform these tasks "intelligently" as well. The above is the primary interest of AI researchers. Situations applicable by game theory are encountered far more often than we expect (ex. car buying).
Economists and game theorists are more interested in how to use game theory as a tool of analysis. It helps us to analyze situations more rationally and formulate an acceptable alternative with respect to circumstance. Game theory helps us to rationalize decisions in dire situation where human emotions may cloud our judgement (ex. Cold War US nuclear strike strategy)
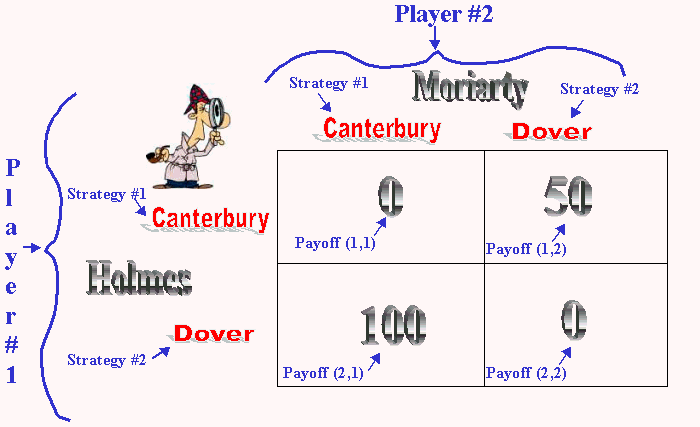
Figure #1: The Payoff Matrix
In order to analyze complex real-world situations, we need some way of encoding the problem and its possible strategies into a mathematical form for computing automata such as a computer. The payoff matrix is used for this purpose. Here, we'll limit our discussion to two-player games; however, the payoff matrix can be made for N-person game. The pure strategy (rational options) for each player is plotted on the axis and the outcome (measured in payoff values based on utility function) is calculated and plotted for each possible pure strategy combinations.
The matrix shown above in figure #1 demonstrates the Holmes vs. Moriarty game as discussed in lecture.
|
Games |
Games can be quite complex; some way of classification is needed to define a game's characteristic. This classification helps theorists to study some particular aspect of a game more closely.
Games can be classified based on:
Player Behavior: Cooperative vs. Conflict
In a zero sum game, the payoffs remain constant through the course of the game play. Two sides are often in conflict in zero-sum games since one player's gain is the other player's loss. Information is critical to success in zero-sum games. Being well informed always helps the player.
In a non-zero sum game, the payoff is not constant during the course of game play. Negative sum games are competitive, but nobody really wins, rather, everybody loses (ex. war or strike). Positive sum games can be cooperative; all players have one goal that they contribute together (ex. OPEC summit).
Players may co-operate or compete, depending on degree of pre-game communication & understanding of the opponent's motive. Non-zero sum games provide this kind of possibility mainly due to the fact that both players may benefit from cooperation.
It is interesting to observe that being well informed may harm a player (ex. blackmail).
The information concerning an opponent's move is well known in advance. All sequential move games are of this type.
Games of Imperfect Information
Partial or no information concerning the opponent is given in advance to the player's decision. Imperfect information may be diminished over time if the same game with the same opponent is to be repeated. As the game progresses, both players gather more and more information about the game itself and his/her opponent's characteristics. Imperfect information may often result in a player conflict even if both stand to gain by cooperation. This is based on the human instinct; "we fear what we do not know".
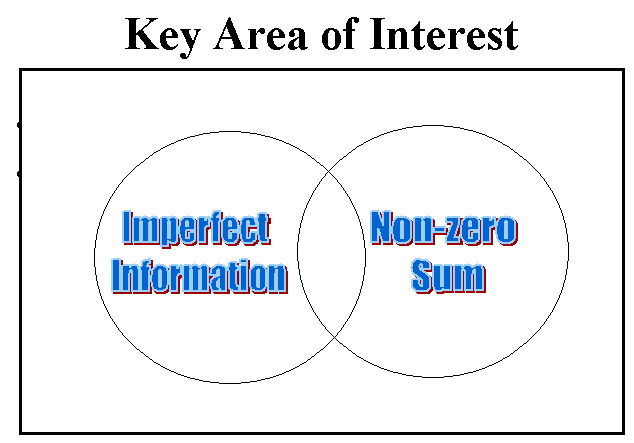
Figure #2: Key Area of Interest
Game theorists are not very interested in games of perfect information at large. It is due to the fact that in games of perfect information, no prediction about the opponent is needed, the optimal move is simply the best available strategy for a given circumstance.
Prisoner's Dilemma
For an example of how a game is classified, the standard Prisoner's Dilemma game would have the following classification characteristics:
Imperfect Information
Two sides competing against each other. It is usually caused by complete lack of information about the opponent or the game. It is a characteristic of zero-sum games.
Players may improve payoff through Communication. The more two players' interests coincide, the more important and advantageous communication becomes. As a result, binding coalitions & agreements are formed before the game.
However, the concept of cooperation is quite tricky. What's best for the whole group is very hard to grasp, and an equilibrium must be reached.
Games of cooperation do not apply to zero-sum games since communication is irrelevant here. There is no possibility of the players cooperating since their interests are exactly opposite.
Prisoner's Dilemma with Iteration
It might seem that the paradox inherent in the prisoner's dilemma could be resolved if the game were played repeatedly. Two versions of iterated prisoner's dilemma are possible:
1) Infinite number of iterations - Both players will cooperate. If one player failed to cooperate in one game, the other player could retaliate by not cooperating in the next game and both would lose until they began to cooperate again.
2) Fixed number of iteration - On the last term, both player will realize that if he/she stops cooperating there is no possibility of the other player retaliate anymore. But then, expecting the other player to do the same on the last turn, the player will try to do this on the second last turn. With domino effect, a "rational" player will actually not cooperate at all starting with the first turn.
Iterated games and mixed strategy leads to Evolutionary Stable Strategy.
|
Basic Game Solving Strategies |
The book "
Thinking Strategically" specifies some simple rules that you can use to help you to come up with an optimal solution to a game. These rules tell you what you need to do, but not how you should accomplish it. We will provide some simple examples and show you how the rules can be applied intuitively. As you can probably imagine, more complex examples would require more mathematically intensive tools to apply the rules.The first rule is "look ahead and reason back." The idea here is that you analyze how the strategies employed by your opponents affect your outcome from the game. You assume that you are playing rational opponents who want to maximize their outcome from the game and that these opponents will also be analyzing you in this same manner. Then, you use this information to "reason back" to what your optimum strategy should be. This rule is actually a general strategy that is applied when applying all other game solving strategies; it's a general strategy rather that a first step to solving games.
The second rule is "If you have a dominant strategy, use it." A dominant strategy is one that gives you a better outcome no matter what strategy your opponents follow. In the example below, your strategy 1 gives you a higher value than your strategy 2 regardless of whether your opponent chooses his strategy 1 or strategy 2; so strategy 1 is dominant and you should choose it.
Figure #3: Dominating Strategy
The third rule is "Eliminate any dominated strategies from consideration, and go on doing so successively." This rule is very useful for simplify a game. What you do here is compare each of your strategies against each of your other strategies and where one is dominated by another for all possible strategy choices of your opponent you eliminate it from the game. You also apply this rule to your opponent's strategy choices. Figure #4 shows the example explained during the presentation. Here you can see that strategy 2 produces for you a lower outcome than strategy 1 for both of your opponent's strategy choices; so you should eliminate your strategy 2 to simplify the game.
Figure #4: Eliminate any Dominated Strategy - Simple example
A more interesting example of simplifying a game using the elimination rule is shown in figure #5. Here, the 6x4 matrix on the left is reduced to the 2x2 matrix on the right. This simplification was done using the following three steps:
Eliminate strategies OS 2 and OS 3 (in blue), since they are dominated by OS 4 (note that being dominated in this context means being lower since you view this step from your opponents point of view).
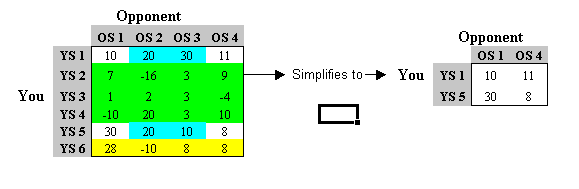
Figure #5: Eliminate any Dominated Strategy - Complex example
The fourth rule is: "Having exhausted the simple avenues of looking for dominant strategies or ruling out dominated ones, the next thing to do is to look for an equilibrium of the game." When you have found an equilibrium you have solved the game. The equilibrium will be your best strategy choice to counter your opponents' best strategy choices. How do you find this equilibrium?
If all players have one dominant strategy, the equilibrium will occur at the intersection of these strategies. This equilibrium is called a dominant strategy equilibrium.
An equilibrium may occur at the minimax or maximin value. Your maximin value can be determined by first analyzing your strategies to determine what the minimum value is that can be returned for each of these strategies. Then, you choose the strategy that maximizes these minimum values. This strategy gives you the maximin value. This value represents the minimum value that you will get no matter what your opponent chooses.
In the example of figure 6, the minimum values for each strategy are placed in the column on the right. These values are 150, -10 and -15 respectively. You will want to make sure that you get at least the maximum of these minimum values, so you will choose strategy 1. This means that no matter what choice your opponent makes you will get at least 150.
Figure #6: Looking for the Minimax/ Maximin values
If you assume that the matrix of figure 6 represents a zero sum game then you and your opponent will be in conflict. Then, from your opponents point of view, she will want to minimize your gains in order to maximize hers. She will therefore look for the maximum value that you will get from each of her strategies and place this value in the row on the bottom of the matrix. Then, she will look for the minimum of the maximum values. This strategy will give her a minimax value that she should choose in order for her to minimize your maximum gains (this also minimizes her maximum losses). Notice that in figure 6 this means that your opponent will choose her strategy 1 so that you will gain no more that 160 no matter what strategy you choose.
Nash Equilibrium is an equilibrium point where neither player will want to change their equilibrium strategy even if they know for certain that their opponents strategy is fixed. In figure #6, above, the minimax strategies for you indicated taking strategy 1 and the minimax strategy for your opponent return her strategy 1. The equilibrium point from this was outcome(1,1) = 150. Now, if you assume that your opponent will not change her mind from choosing strategy 1, you can actually do better by changing to your strategy 3. This would give you outcome(3,1) = 160. There is no Nash Equilibrium in this situation from pure strategies.
The boxed pig game of figure #7 does have a pure strategy Nash Equilibrium
(select this link for an explanation of the boxed pig game). Before showing the Nash Equilibrium let's review what the pure strategy equilibrium point is. Notice that the little pig has wait as a dominant strategy since she will get 4 from waiting when the big pig presses versus 1 by pressing when the big pig presses. Also, she will get 0 by waiting when the big pig waits versus -1 by pressing when the big pig presses. Therefore, it is a given that the little pig will wait. Since the big pig knows that the little pig will wait he will decide that his best choice is to press. He determined this by noticing that he will get 5 from pressing and only 4 from waiting. The pure strategy equilibrium point from the game = outcome(press, wait). Is this a Nash Equilibrium?Let's check. Assume first that the little pig will choose wait for sure. Then the big pig will choose press as we previously determined. Okay then, let's now assume that the big pig chooses press for sure; will the little pig now change her strategy? No, we determined previously that the little pig has wait as a dominant strategy. Hence, this is definitely a pure strategy Nash Equilibrium.
Figure #7: Nash equilibrium and the Boxed Pigs Game
Sometimes an equilibrium to the game can't be found in pure strategies. In these situations it may be better to alternate (mix) your strategy choices in a probabilistic fashion. This is the case in the game shown in figure #8. Here the guard must protect both safes. He can't be in two places at once so if he chooses to protect only safe 1 (since it has more money in it), the thief will have free access to the $10,000 in safe 2. If, however, he decides that he will mix his strategies such that he will randomly be at safe one 10/11 of the time and at safe two 1/11 of the time (these proportions are determined by the comparing the money in each safe to the total money in both safes) he can reduce the expected value that the thief will get to $9,091. (
Select this link to see the mixed strategy calculation.)Figure #8: Mixed Strategies
|
Evolutionary Games |
In evolutionary game theory we use an iterated model to determine what the best strategy is. We use random assignments of various strategies to members of the population to simulate possible choices. Under this system, random interactions replace rational behavior. The best strategy is the one that is the fittest to survive over time. We don't need to find the best strategy since this may take several thousand iterations of the game. After just a few iterations, a good strategy will start to emerge. We should use evolutionary game theory for two reasons: first, we may not have adequate resources to search through all possible strategies; and second, there may not be an easy way to find an equilibrium. Though evolutionary theory deals with the interactions of a population, we still consider all competitions between members of the population as strictly two person games.
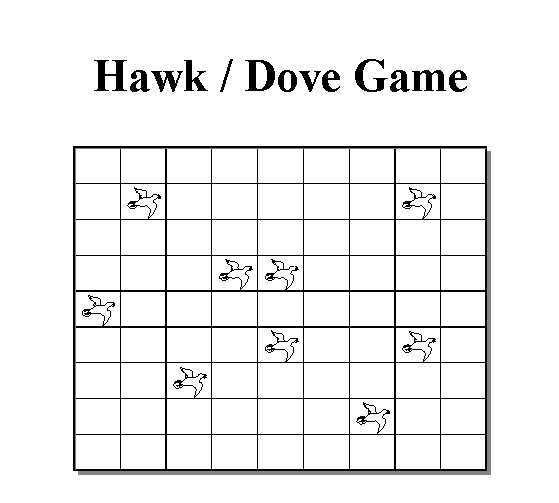
Figure #9: Hawk/Dove Game
The Hawk and Dove game is a simulated ecosystem for a population to interact within. Players move around the grid and compete for resources with other members if they are in adjoining squares. Players compete for resources, they do this by choosing a strategy from one of two possible ones:
Hawk strategy - an aggressive strategy, will always escalate conflict.
Dove strategy - a non-aggressive strategy, always avoids conflict.
This is similar to the behavior of animals in nature, they may also choose from one of two strategies, they can choose to be aggressive and fight for available resources, or they can chose to cooperate and share the available resources. Players can adopt either a pure or a mixed strategy, they must choose the percentage of time they will behave like either a Hawk or a Dove. Individual players' fitness is determined by their accumulated payoffs over time. The game can be simulated by either having a set population strategy and allowing mutations within this strategy, or we can have a well-distributed strategy set among the population at the beginning of the game and see what strategy survives.
Evolutionary Stable Strategy (E.S.S)
The idea of an evolutionary stable strategy was introduced by Maynard Smith and Price in 1973, the idea behind it is that after an elapsed time a strategy will become predominant in a population. This strategy becomes predominant because it is the best strategy for the population to adopt. In fact, it is so successful that any mutations within the population become ineffective because they are deemed to be less fit to survive than any members of the existing population are. Smith and Price developed this idea through observations of animal behavior. It would seem that aggressive behavior would give a natural advantage to those who display it, Smith and Price wanted to explain non-aggressive and cooperative behavior in animal populations. It is important to note that not all members of the population must adopt the Evolutionary Stable Strategy; there may be those members of the population who adopt differing strategies. However, a strategy is deemed to be a stable one if the entire population's average strategy is equal to that strategy. So if at any given time we can expect that n% of the population are adopting a certain strategy, on average, then that will be the Evolutionary Stable Strategy for the population.
Payoff Matrix for Hawk and Dove Game
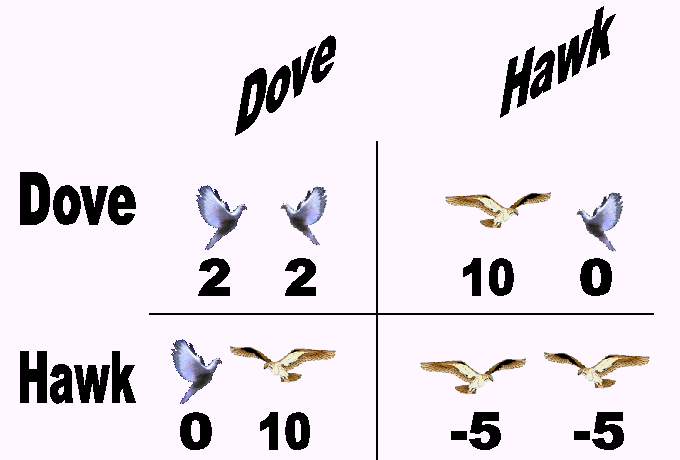
Figure #10: Payoff Matrix for Hawk/Dove Game
The Hawk and Dove Game is a zero sum game, this is the case because though the players are competing for resources, they re taking the resources from their environment, not from each other. There is a cooperative strategy available in the matrix that is the Dove-Dove strategy. The question here is which strategy is the Evolutionary Stable Strategy for this payoff matrix. If we look at the two possible pure strategies, we can see that the pure Dove strategy (Dove 100% of the time) looks like it would be a good strategy overall. We say this because if every member of the population was to adopt it we would have a good cooperative strategy where all members of the population would benefit equally. The problem with this strategy, however, is that it is not stable against mutations within the system. That is, if a mutation were to occur, such as the appearance of a pure Hawk strategy, this new strategy would have the advantage over the rest of the population since it would always be competing with Doves for resources. This new mutation would survive because its fitness level would be higher than the rest of the population so we can see that this strategy is not evolutionary stable. As for the other possible pure strategy (Hawk 100% of the time), we can see that although a player adopting a pure Hawk strategy would have an advantage over any opponents that choose a Dove strategy, against others who also choose a Hawk strategy it would loose a great deal. Therefore a pure Hawk strategy is not the solution either. Therefore our Evolutionary Stable Strategy must be a mixed strategy, the question is how do we determine what this strategy should be?
Figure #11: ESS of Hawk/Dove Game
We can represent the payoff matrix on a graph, this is done by plotting any member of the population's expected payoffs for each of the it's possible strategies given what percentage of the rest of the population adopts a Dove strategy at any given time. If we look back at the payoff matrix for the Hawk and Dove game, we can see that if any member of the population were to choose a Dove strategy, and if 0% of the rest of the population were to choose a Dove strategy (100% were to choose a Hawk strategy), then that members expected payoff would be 0 each time it competed for resources. However, if 100% of the rest of the population were to choose a Dove strategy (0% were to choose a Hawk strategy), then that members expected payoff would be 2 each time it competed for resources. We then plot the pink line for this expected payoff. We can do the same for the Hawk strategy, which will range from -5 if 0% choose a Dove strategy to 10 if 100% choose a Dove strategy. The point where these two lines intersect is the % of population that must choose Dove (on average) to have an Evolutionary Stable Strategy. So we can see for this payoff matrix that our Evolutionary Stable Strategy is about 38.5 % Dove and 61.5 % Hawk. If our two plotted lines did not cross, this could only be because we had a dominating strategy that would be the one with the higher of the two lines on the graph. This method works well for two possible strategies; however, if we have three possible strategies to choose from we must plot these on a three-dimensional graph which is much more difficult to do. In order to determine what the Evolutionary Stable Strategy would be if we had more than two possible strategies, we can simply run the game over enough generations and by eliminating strategies that give the lowest payoffs and reproducing those with the highest, we can let the system develop it's Evolutionary Stable Strategy on its own.
|
Where is Game Theory Currently Used? |
Game theory is currently used in many key areas; some examples of this are is ecology, networks and economics. It can be used in ecology to model an ecosystem. Much like the Hawk and Dove game, we can simulate the interactions of animals in nature. To do this the payoff matrix must be determined first; studying animals in nature and approximating what their payoffs will be can do this. In networks, game theory can be used in congestion control for determining what is the best means to route communications through a system. Game theory can also be used in economics. Economists are very interested in how people interact, and in the idea of supply and demand. The stock market, though extremely complicated, can be viewed using game theory. We can see that if someone had a bad strategy of buying and selling on the stock market they would not survive for long amongst fierce competition.
|
Limitations and Problems |
There are some limitations and problems to game theory that make its applicability to modeling behavior imperfect at best. Game theory assumes all players will want to maximize their outcomes; however, real people don't always make rational choices. In the case of the Indiana Jones example, there were other choices available to Indiana. He could have committed suicide by intentionally choosing a grail he did not think to be correct or he could have just run away from the situation, but since these are not logical choices, game theory does not consider them. Another problem for game theory is that a utility cannot always be provided for all outcomes. Utility itself is an imperfect tool; for example, in the game of chess, if the pieces are to be assigned a certain numerical value at the beginning of the game, this utility may change over the course of the game. A pawn is given a relatively low value at the beginning of the game. At a later point in the game, if it is in a position to put the opponents king in check or is close to reaching the opponents end and becoming a queen, then it's value will be greater. This changing value is difficult to calculate and because it requires a full understanding of the game as a whole, can be as big a problem as playing the game itself. Another problem for game theory is that some payoffs can't be quantified, there are other factors that determine behavior such as morality. People don't always make the greedy choice even though these choices do not appear to be in their best interests.
|
Summary |
Below the major concepts that we have presented in these web notes are summarized briefly:
Game Theory
- The mathematical analysis of multi-player interactions where the players are required to make strategic choices to obtain the best possible outcomes from their interactions.Rationality
- Game theory assumes that the "rational" of players is to maximize their outcomes.Utility
- Utility is the measure of a game player's preference towards certain outcome.Payoff Matrix
- In a 2 player interaction the rows of the payoff matrix represent the strategies of player 1, the columns of the matrix represent the strategies of player 2, and the cells of the payoff matrix contain the interaction outcomes for player 1 based upon the row/column strategy selection of each player. In the case where the cells contain 2 values separated by commas then the first number is the outcome for player 1 and the second number is the outcome for player 2.Basic Strategies
- The basic strategies presented above help you simply or solve the game.Plan Ahead and Look Back
- This just says that you must analyze your opponent's strategy selection process to help you choose your own strategy selection process.Dominant Strategy
- A strategy that gives you a better outcome than any of your other strategies can regardless of what your opponent does. (Your opponent can also have a dominant strategy of her own.)Dominated Strategy
- A strategy that you want to eliminate from the payoff matrix since it is worse than another strategy you have no matter what your opponent chooses.Equilibrium
- The point at which your best strategy and your opponents best strategy meet.Dominant Equilibrium
- If both players have a dominant strategy, the equilibrium is at the matrix cell where these strategies intersect.Minimax value
- From your point of view on your matrix, if each of your strategies is analyzed according to the maximum possible loss it can provide and you choose the strategy giving the minimum of these loss values, then this value is your minimax value. From your opponents point of view on your matrix, if each of your opponents strategies is analyzed according the maximum possible gain you can obtain from it, she will choose the minimum of these maximum gains to get her minimax value.Minimax strategy - T
he strategy that returns either a minimax or a maximin value. This is the most conservative strategy.Maximin value
- From your point of view on your matrix, if each of your strategies is analyzed according to the minimum possible gain it can provide and you choose the strategy giving the maximum of these gain values, then this value is your maximin value. From your opponents point of view on your matrix, if each of your opponents strategies is analyzed according the minimum possible loss you can obtain from it, she will choose the maximum of these minimum gains to get her maximin value.Nash Equilibrium
- An equilibrium point where neither player will want to change their equilibrium strategy even if they know for certain that their opponents strategy is fixed.Mixed Strategies
- A player strategy that will choose a variety of their pure strategies in a probabilistic fashion.Pure Strategy
- A player strategy that can be represented along either a column or row of the payoff matrix.Zero-sum game
- In a 2 player game this is represents a game where one players winnings equal the other players losses.Non-zero-sum game
- A game where all players can win and/or all players can lose at the same time.Cooperation game
- A game where some or all of the players can discuss in advance what strategies they are going to use.Conflict game
- A game where two players compete against each other.Perfect Information game
- A game where one player has access to complete information concerning the other player's move and his/her environment factors.Imperfect Information game
- Games not classified as Perfect Information.Evolutionary Stable Strategy
- A strategy that will survive in the long run of an iterated game regardless of the other players' strategies employed.![]()