Proofs That Languages are Undecidable or Unrecognizable
Overview
This next set of lectures concerns the question of whether there are problems that provably cannot be solved by computers, and how to identify these.
Two techniques for showing that languages are undecidable, or unrecognizable — which make use of closure properties for the sets of decidable languages and of recognizable languages — will be introduced.
This material will be covered in lectures on October 16–30 and in tutorials on October 27 – November 4.
Supplemental Material
You should not need any reference material, for this, that is not provided on the course web site. However, the following book provides a readable introduction to computability theory, including the use of many-one reductions to prove undecidability:
- J. E. Hopcroft, R. Motwani, and J. D. Ullman,
Introduction to Automata Theory, Languages, and Computation
Third Edition, Pearson/Addison-Wesley, 2007
Lecture #13: Universal Turing Machines (Thursday, October 16)
Why This is Included
A “Python emulator” is a program that receives a Python script and input for that script, and executes the script on the input. This can be written as a Python script, itself.
Similarly, a “Java compiler” is a program that receives a Java program as input and converts it into lower-level machine code that can be processed, directly, by a computer. This can be written as a Java program, itself.
This lecture introduce a universal Turing machine — which is, essentially, a “Turing machine interpreter” which is, itself, a Turing machine.
Once one knows about universal Turing machines, one can define an “acceptance language”, ATM, and prove that it is recognizable. A simple proof by contradiction establishes something extremely important, namely, that this language is undecidable. The complement of this language is provably unrecognizable — and proofs of both of these results are also sketched.
Thus, this lecture plays a role that is similar to the lecture about regular languages that introduced the Pumping Lemma for Regular Languages, as part of the discussion of regular languages: It introduces the first provably undecidable and unrecognizable languages, that are needed in order to use techniques, introduced after this, to prove that other languages ore undecidable or, sometimes, unrecognizable, as well.
Preparatory Viewing and Reading
Lecture Presentation
Lecture #14: Oracle Reductions (Tuesday, October 21)
Why This is Included
“Establishing an oracle reduction” is the first technique to prove undecidability, that is based on a closure property, which will be introduced in this course. This is often the first such technique introduced, in introductions to computability, because it can be easier to discover and present oracle reductions than the other kind of “reduction” that will be introduced after this. As this lecture explains, oracle reductions can be used to prove that various languages are undecidable if you know of at least one undecidable language already.
Preparatory Viewing and Reading
- Oracle Reductions [ Video: 20:39 ]
- Oracle Reductions — Supplement for Preparatory Viewing [ PDF: 1p. ]
- Oracle Reductions — Key Concepts [ PDF: 2pp. ]
Lecture Presentation
Tutorial #13: Oracle Reductions (Monday, October 27 and Tuesday, October 28)
Lecture #15: Many-One Reductions (Thursday, October 23)
Why This is Included
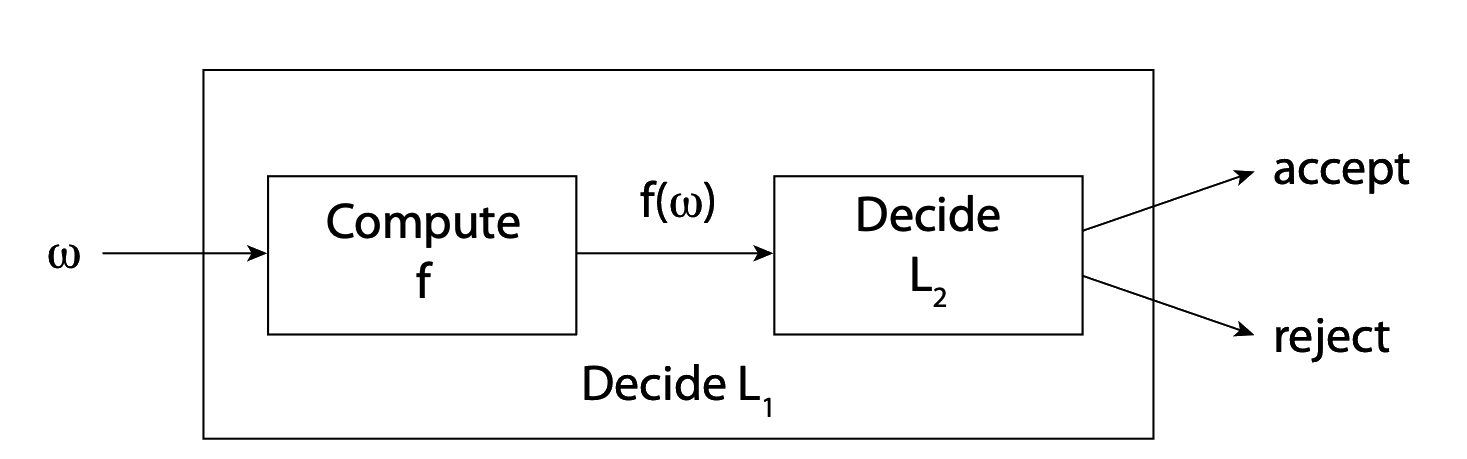
While oracle reductions can be used to prove undecidability, because the set of decidable languages is closed under these reductions, the set of recognizable languages is not closed under these reductions, so they cannot be used, in the same way, to prove unrecognizability. Many-one reductions between languages can be trickier to find and describe — but the set of recognizable languages is closed under these reductions, so that many-one reductions can be used to prove unrecognizability and to prove undecidability.
The lecture also introduces decision problems — which we are frequently interested in, instead of languages, describes what it means to “prove that a decision problem is undecidable”, and outlines a process to do this too.
Preparatory Viewing and Reading
- Many-One Reductions [ Video: 36:12 ]
- Many-One Reductions — Supplement for Preparatory Viewing [ PDF: 3pp. ]
- Many-One Reductions — Key Concepts [ PDF: 4pp. ]
Lecture Presentation
Tutorial #14: Many-One Reductions I (Wednesday, October 29 and Thursday, October 30)
Lecture #16: Proof of Undecidability — Examples I (Tuesday, October 28)
Why This is Included
Students can find the problem of proving undecidability of decision problems to be overwhelming — there can be too much to keep track of. However — as the previous lecture presentation tried to explain — this information can all be managed, if you start at the high level and solve the problem from the top down.
This lecture provides another example of a proof of undecidability — which resembles the kind of problem that students might be asked to solve on an assignment for this course — so that students can be more familiar with the process that you are being asked to follow.
Preparatory Reading and Viewing
- Proofs of Undecidability: Examples I [ Video: 18:11 ]
-
Proofs of Undecidability: Examples I — Key Concepts
[ PDF: 1p. ]
- Supplement: A Useful Subroutine [ PDF: 7pp. ]
Lecture Presentation
Lecture #17: Proofs of Undecidability — Examples II (Thursday, October 30)
Why This is Included
Sometimes, one example is not enough. This lecture will include another “many-one reduction” resembling those that you might be asked to give when solving a problem on an assignment. It is slightly more complicated that something that might be required for an assignment — the mappings you will need to describe will generally be simpler than the one that is used here.
Preparatory Viewing and Reading
- Proofs of Undecidability: Examples II [ Video: 26:37 ]
- Proofs of Undecidability: Examples II — Key Concepts [ PDF: 1p. ]


